時系列データでトレンドを持つ場合の中に、単位根過程やトレンド定常過程というものがあります。
単位根過程の場合は、階差を取れば、定常過程に
することができ、その判断のために単位根過程であることを把握したい場合、ADF検定を行います。
コード
ADFはstatsmodelsに実装されています。
単位根過程であることを帰無仮説に検定を行います。
from statsmodels.tsa.stattools import adfuller adf,pvalue,usedlag,nobs,critical_values,icbest = adfuller( x = data, regression=, maxlag=, autolag = ) print( adf, pvalue, usedlag, nobs, critical_values,icbest )
引数としてはいくつまでのラグを対象にするかmaxlag,ラグ選択に用いる値autolag,トレンド構造などを指定するregressionがあります。
regression種類は
- c : 定数のみ
- ct : 定数 + 線形トレンド
- ctt: 定数 + 線形トレンド + 非線形トレンド
- nc: なし
となります。
戻り値としては adf(統計量)とcritical_valuesを比較すれば良いですが、p値をそのまま見せるほうが、統計量がわからないが、検定の概念を知っている人にはいいかもしれません。
試してみる
データの発生
a1 = 1のとき単位根過程となります。
import random def create_data(y0,a1): yn = y0 data = [] for i in range(100): yn = a1 * yn + random.random() data.append(yn) return data #data2は単位根過程 data = create_data(3,0.2) data2 = create_data(3,1) data3 = create_date(3,0.9)
可視化してみておく
import matplotlib.pyplot as plt fig,axs = plt.subplots(3,1) for ax,d in zip(axs,[data,data2,data3]): ax.plot(d)

data2はがっつりトレンドがありますね。
検定してみる
構造と各データごとに繰り返すのがめんどくさいので、関数を作って実施してみます。
また、単位根過程は階差をとれば定常になるはずなので、data4もつくって試します。
from statsmodels.tsa.stattools import adfuller def my_adf(d): ps = [0.01,0.05] for reg in ['nc','c','ct','ctt']: adf,pvalue,usedlag,nobs,critical_values,icbest = adfuller( x = d, regression = reg, autolag = 'AIC' ) ps.append(pvalue) return ps fig,axs = plt.subplots(4,1) #a1=1のケースの階差をとる data4 = pd.Series(data2).diff().dropna() for ax,d in zip(axs,[data,data2,data3,data4]): ax.bar(height=my_adf(d),x='0.01,0.05,nc,c,ct,ctt'.split(','))
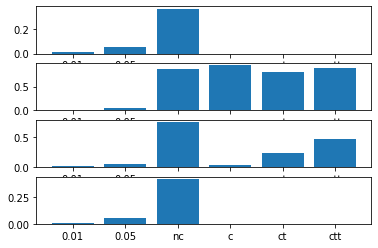
data2では棄却できませんでしたが、それ以外では棄却できるパターンがあることがわかりました。