Pythonでネットワーク構造のデータを扱いたい(networkxを扱う)

データ分析の仕事をしていると、基本的な表形式のデータ以外では表現しにくい現実事象が存在します。要素と関係性で表現されるネットワークもその一つです。

個人的にはこの形式のデータは、示唆までたどり着きにくいため、ビジネス的な分析とは言いにくいな、とは思います。ただし、探索的にデータを理解したり、プロダクトの機能として使えることは多い分野だと思っているため、タイトルはあえて「データを扱う」にしました。

ネットワーク分析とは

networkxはグラフ(ネットワーク)に関するデータの保持/操作をしやすくするパッケージです。

なお、情報がきちんとまとまっているのは以下の書籍です。(クリックするとAmazonにとびます)
（感染症のモデルであるSIRモデルや、Word2Vecとの組み合わせなど、応用も多く非常に面白かったです。

ネットワークは繋がりを持つ要素(=ノード)と、その繋がり(=エッジ)で表現されます。このノードとエッジは重さや属性といったものを持ちます。

このネットワーク、ノード、エッジを把握しつつ、これらの各指標を定量化/分析する手段がネットワーク分析です。

使い方

上で書いた通り、ネットワーク、ノード、エッジといったデータの保持と、各指標の集計を行う機能を持ちます。

まずはデータの作成と、可視化です。

import networkx as nx

#ネットワークの作成
G = nx.Graph()

#エッジとノードの定義
#数字がノード
#1,2は二つをつなぐエッジ
#weightはエッジの属性
edges = [
         (1,2,{'weight':0.1}),
         (1,3,{'weight':0.1}),
         (1,4,{'weight':0.1})
        ]

#エッジとノードをグラフに追加
G.add_edges_from(edges)

#上記でエッジとノードを一気にいれたがノードを先に入れておくこともできる
#G.add_nodes_from([1,2,3,4])

#ノードへの属性追加もできる
#G.nodes[1]['color'] = 'red'

#描画
nx.draw(G)

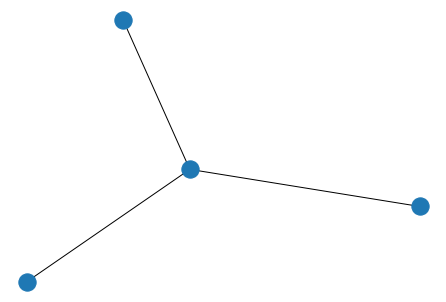
各指標を取り出したり、それぞれの情報を探索もできます。
もちろん、このくらいなら、基礎集計からつくれなくもありませんが、数が増えたり、より高度なことをやったり標準化する上ではnetworkxを使うメリットは大きくなります。

#ノードの数
print(G.number_of_nodes())

#エッジの数
print(G.number_of_edges())

#ノード1の接続数(次数)
print(G.degree[1])

#ノード1に繋がるノード名
print(list(G.adj[1]))

仮想データで使ってみる

自分がソーシャルサービスを使っているとか仮定して、データを見てみます。

データをつくる

ユーザーは100人でいて、彼らはランダムな数のつながりを持っているとします。1ユーザは平均3、偏差2の正規分布にしたがってつながりを持ちます。

import random

class User:
  def __init__(self,id,N):
    self.id = id
    self.connect_num = round(random.gauss(mu=3,sigma=2))

    #自分以外の誰かとランダムに繋がりをもつ
    users = [i for i in range(N) if i != self.id]
    random.shuffle(users)
    self.connect_user = users[:self.connect_num]

#ユーザデータの生成
N = 100
users = [User(i,N) for i in range(N)]

グラフ構造にする

import networkx as nx
G = nx.Graph()

edges = []
for u in users:
  for c in u.connect_user:
    G.add_edge(u.id,c)

nx.draw(G)

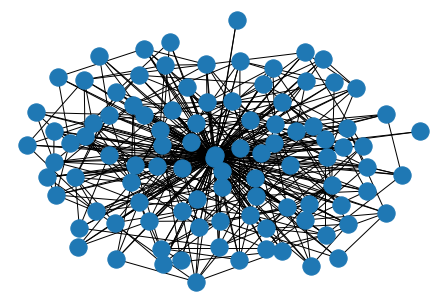
一応描画しますが、このくらいになるともう目で見ても何もわかりません。ので、指標をみたりすることで全体を把握します。

探索など

ノードのつながり数の分布を把握してみます。

print(G.number_of_nodes())
#100
print(G.number_of_edges())
#476

import matplotlib.pyplot as plt 
plt.hist([x[1] for x in list(G.degree)],bins=30)

繋がりの数は476、1ノードあたり平均3しか繋がりは生まれず、複数回でるつながりは1になるはずですが、実際は1ノードあたり平均5弱の繋がりが生まれています。

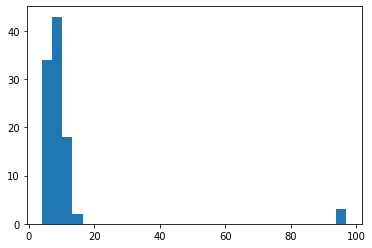ヒストグラムを見ると、どうやら100近いものがいるようですが(100ノードしかないので、ほぼ全員とつながりがあるということです)、大半は10程度のつながりのようです。このように、繋がり数(=次数)をヒストグラム、平均、中央値など一般的な集計値で定量化し、考えやすくなっています。

特徴がありそうなノードをみてみる

#エッジ数でノードをソートした上位5つ
sorted( dict(G.degree).items(),key = lambda x:x[1],reverse=True)[:5]
# [(34, 98), (21, 98), (48, 16), (92, 13), (9, 12)]

ノード34,ノード21が98も繋がりを持っているようですね。

node_name = 34
print(G.degree[node_name])
print(list(G.adj[node_name]))

こんな感じでノードの次数や、繋がるノードを探索できます。
こうした構造のデータを扱うシステムを作る時に手軽に作れます。

もう少し探索できるようにしてみる

つながりは、縦横にユーザーid、値に繋がり有無のテーブル構造をつくれば、類似度などを出すことができます。
ここからもちろんクラスタリングなどにつなげますし、ひとまず、似た繋がりを持つユーザーを検索できるように、ユーザー間の類似度を計算してみます。

#pivotするために適当なカラム名とフラグを与える
df = pd.DataFrame(list(G.edges()),columns = ['row','col'])
df['exist_flg'] = 1

#pivot
tb = df.pivot_table(index='row',columns='col',values='exist_flg',fill_value=0)

import scipy.spatial.distance
import numpy as np

node_num = 5
dist_node = 10

#コサイン類似度
1 - scipy.spatial.distance.cosine(np.array(tb)[node_num],np.array(tb)[dist_node])

こんな感じで、全体の把握->ノードの指標->つながりの数からノードの類似度の計算までを行うことができました。

▼もう少し応用してクラスタリングをしたい時はこちら

esu-ko.hatenablog.com